ML perceptron

• Input & output
• Main idea
• Learning method
• Halt proof
• Example in practise

Perceptron is a linear classifier which is the basis of SVM and neural network.

Input & output

the input $x=(x_{1},x_{2},...,x_{d})$, d is the dimension of feature vector x.

the output $y = \{+1, -1\}$, y is the true / false label set.

Main idea

$h(x) = sign( \sum_{i=1}^{d}w_{i}x_{i} - threshold)\\ = sign( \sum_{i=1}^{d}w_{i}x_{i} + (-threshold) \cdot (+1))\\ = sign( \sum_{i=1}^{d}w_{i}x_{i} + w_{0}\cdot x_{0})\\ = sign( \sum_{i=0}^{d}w_{i}x_{i})\\ = sign(w^{T}x)$

The only thing is about the trained weight matrix $w$.

Learning method

First, randomly initialize the $w$, then correct it via the samples that are wrongly classified.

1.When the training step is $t$, the matrix is $w_{t}$, then a mistake point $(x_{i}, y_{i})$ can be checked via the following condition

$$sign(w^{T}x_{i}) \neq y_{i}\\ or : y_{i}w^{T}x_{i} \lt 0$$

2.The next step is to correct $w_{t}$, the M is the wrongly classified points set, there are two ways of thinking:

• Stochastic gradient descent
    considering the natural solution is to set the number of the wrongly classified points as loss function, but it is not easy to optimize, so to use the cumulative distance of all wrong points instead.

  The distance of point $(x_{i}, y_{i})$ to the line $w^{T}x = 0$ is

$$\frac {\vert w^{T}x_{i} \vert}{\Vert w \Vert}$$

  The cumulative distances of wrong points to the line $w^{T}x = 0$ is

$$\frac {- \sum_{x_{i} \in M} y_{i}w^{T}x_{i}}{\Vert w \Vert}$$

  Simplify the $\Vert w \Vert$, the loss function is

$$- \sum_{x_{i} \in M} y_{i}w_{t}^{T}x_{i}$$

  do SGD, get the update rule

$$w = w + \sum_{x_{i} \in M} \eta y_{i}x_{i}$$

  (Note that here we can also set learning rate $\eta$ when update, default is 1.)

• Two-dimension illustration

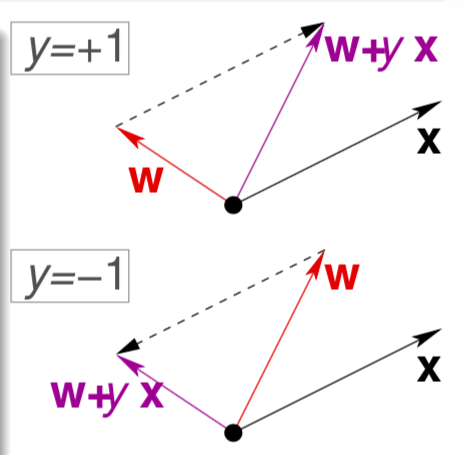
When the point $(x_{i}, y_{i})$ is wrongly classified, if the true label is +1, then the false $w_{t}^{T}x_{i} \lt 0$, it means the angle between $w_{t}$ and $x_{i}$ is larger than 90 percent, then do $w_{t} + x_{i}$ will lower the angle.

For another side, if the true label is -1, then the false $w_{t}^{T}x_{i} \gt 0$, it means the angle between $w_{t}$ and $x_{i}$ is less than 90 percent, then do $w_{t} - x_{i}$ will enlarge the angle.

So the update rule should be $w_{t} + y_{i}x_{i}$.

Halt proof

Since we know to update is to correct, to get closer to the perfect classifier, and there do exists a perfect $w_{f}$ to stop the training process, then it is necessary to prove the process of learning will halt.

1.First, since $w_{f}$ is the perfect weight matrix, the space is $y = w_{f}^{T} x$, there should be an instance $(x_{n}, y_{n})$ that is closest to the space.
For any instance $(x_{i}, y_{i})$,

$$y_{i}w^{T}x_{i} \ge \max_{n} y_{n}w^{T}x_{n} \ge 0$$

Then to update by correcting the point $(x_{m}, y_{m})$,
$w_{f} \bullet w_{t+1} = w_{f} \bullet (w_{t} + y_{m} \bullet x_{m})\\ \ge w_{f} \bullet w_{t} + \max_{n} y_{n}w^{T}x_{n}\\ \ge w_{f} \bullet w_{t} + 0$

It means that $w_{f} \bullet w_{t+1}$ is getting larger, but we still need to prove that the ${\Vert w_{t+1} \Vert}$ is not getting too large, then it can be proved the angle between $w_{f}$ and $w_{t}$ is getting smaller.
${\Vert w_{t+1} \Vert}^{2}\\ = {\Vert w_{t} + y_{m} \bullet x_{m} \Vert}^{2}\\ = {\Vert w_{t} \Vert}^{2} + {\Vert y_{m} \bullet x_{m} \Vert}^{2} + 2 \bullet y_{m}w_{t}^{T}x_{m}\\ \le {\Vert w_{t} \Vert}^{2} + \max_{n} {\Vert x_{m} \Vert}^{2} + 0$

2.How many times to update until halt? That is to calculate the following formula: $\frac {w_{f}^{T} w_{t}}{ {\Vert w_{f} \Vert} {\Vert w_{t} \Vert}}$ given, $\rho = \min_{n} \frac {y_{n}w_{t}^{T}x_{n}}{\Vert w_{f} \Vert}\\ R^{2} = \max_{n} {\Vert x_{n} \Vert}^{2}$
since,

$${w_{f}^{T} w_{t}} \ge T \bullet \min_{n} y_{n}w_{t}^{T}x_{n}\\ = T \bullet \rho {\Vert w_{f} \Vert}\\ \\ {\Vert w_{t} \Vert}^{2} \le T \bullet \max_{n} {\Vert x_{n} \Vert}^{2}\\ {\Vert w_{t} \Vert} \le \sqrt[2]{T \bullet R^{2}}\\$$

so

$$\frac {w_{f}^{T} w_{t}}{ {\Vert w_{f} \Vert} {\Vert w_{t} \Vert}}\\ \ge \frac {T \rho {\Vert w_{f} \Vert} }{ {\Vert w_{f} \Vert} \sqrt[2]{T \bullet R^{2}} }\\ T \le \frac {R^{2}}{\rho^{2}}$$

Example in practise

IPython file

Goodbye!

---